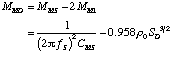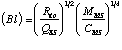|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Of Mass And Resistance
by Ahmet Deniz
I recently set about designing a passive subwoofer for a pair of commercially available mini-monitors that I own.* The mini-monitor in question is mercilessly accurate and revealing, but like all mini-monitors it has limitations in its bass response. The bass it produces is clean and, considering the tiny dimensions, surprisingly deep. But, unfortunately, not quite deep enough to be completely satisfying. I decided to solve this problem the same way the original manufacturer did--by designing a dedicated passive subwoofer. The manufacturer’s purpose-designed subwoofer works very, very well, but unfortunately it is very, very costly and is no longer being made. So, I figured that if I wanted a quality subwoofer extension, I would have to build my own. In the process of designing the sub, I made some derivations of Small’s and Thiele's original equations that I thought might be of interest to some builders. The equations I describe in this article will be of interest to anyone who has been frustrated by not being able to find a catalog driver to meet a situation's given requirements. Although the derivations are specific to the needs I encountered in my subwoofer project, my hope is that you will be encouraged to use similar derivations for other situations you may encounter. SENSITIVITY MATCHING. The big problem I had was finding a driver with an appropriate sensitivity. To produce a flat system response, the sensitivity of the add-on subwoofer needed to match the sensitivity of the mini-monitor satellites. (Remember, this was to be a passive subwoofer.) The manufacturer of my mini-monitors specifies a sensitivity of 85 dB for 2.83 volts input at 1 meter--a figure I verified in testing. The subwoofer would be closely coupled to the floor of my room and so would be seeing an approximately hemispherical load. This meant that I needed a driver with a hemispherical sensitivity close to 85 dB if I wanted to put it in either a closed or vented box. If you page through the various catalogs of drivers available to home builders, you will find very few low-frequency drivers with a specified sensitivity near 85 dB. Most drivers are considerably more sensitive. While insertion losses in the crossover would reduce the effective sensitivity a bit, these losses would typically be limited to about a decibel--not much of a help. Of the drivers I did find with an appropriate sensitivity, none of them gave me the kind of extension I wanted. Now what? One obvious course of action was to modify the performance of a selected off-the-shelf driver to meet my needs. Speaker Builder authors have previously dealt with modifying drivers using series resistance and by adding mass to driver cones [1],[2]. While these articles have presented some general rules of thumb for determining how a given resistance or mass will affect a driver's parameters, my project required a concise, analytical approach to accurately predicting outcomes. Luckily, it is not impossible to develop such an approach. If we take the original Thiele/Small (T/S) equations that describe a driver's low frequency behavior and apply some basic knowledge of how loudspeakers work, we can derive a set of equations that tell us exactly what we want to know. In this case, what we want to know is how much mass and/or resistance we need to add to driver of known specification to achieve a given sensitivity. We will also want to know what impact that added mass and/or resistance will have on that driver's T/S parameters. I will first present the analysis that leads to the equations we need, and then I will follow that with a design example to show you how to use the equations. BACK TO THE BASICS. The first step in our analysis is to think about how a driver works at a fundamental level. At its core, a loudspeaker is a system consisting of a mechanically resonant diaphragm/voice-coil assembly driven by an electromagnetic motor. As such, we can view the driver as having a set of "Fundamental Parameters" directly reflecting the above two subsystems, and it turns out that doing so simplifies our analysis quite a bit. To that end, I have tabulated a set of Fundamental Mechanical Parameters in Table 1 and a set of Fundamental Electromagnetic Parameters in Table 2. (These parameters are based on the analysis of electrodynamic loudspeakers given in Beranek's "Acoustics" [3].) Some discussion of these parameters is now in order.
Simple mechanically resonant systems can be characterized as having a moving mass, a compliance, and a loss factor--a measure of the amount of energy in the mechanical system that is converted to heat from kinetic and potential energy. In a loudspeaker driver, almost all of the system's moving mass comes from the diaphragm and the voice coil assembly, and we refer to this mass as MMD. The mechanical compliance comes from the combined effect of the driver's surround and spider, which we have lumped together into the parameter CMS. The mechanical losses (which arise primarily from friction and viscous losses in the surround and spider--but also from resistance to air flow around the voice-coil and other more subtle phenomena) are approximated by the simple mechanical resistance RMS. A driver's diaphragm has an effective surface area, the relevance of which will become clear below, which we refer to as SD. The parameter MM1 is the result of a rather subtle phenomenon that we nonetheless need to account for. Wave your hand in the air. You should be able to sense that there is something there that oh-so-slightly impedes your hand's motion, namely the gazillions of air molecules that you're displacing with your hand. The faster you wave your hand (i.e., the greater the frequency of your waving) the more impedance you seem to feel. Not surprisingly, a loudspeaker's diaphragm experiences much the same thing, and this thing is typically identified as "radiation impedance" in the technical literature. The nature of this impedance is actually rather complex--in many senses of the word. Fortunately, after applying some of the approximations that acousticians routinely depend on to get usable analytic relations, it can be shown that at low frequencies the effect of the impedance brought on by the air load on a diaphragm is almost exactly equivalent to adding a small physical mass to the cone. This equivalent additional mass experienced by one side of a diaphragm mounted on an infinite baffle is represented by MM1 and is equal to
where p0 represents the mean density of air (typically about 1.18 kg/m3). Finally, MMS represents the total effective mass of the entire moving system and is equal to sum of MMD and two MM1 (one for each side of the diaphragm).
A loudspeaker's electromagnetic motor essentially consists of an electrically conductive coil (i.e., the voice coil) placed within a magnetic field. The strength of the magnetic field (or more correctly, the strength of the magnetic field cutting the voice-coil at a right angle) is represented by B, the air flux density . The length of the wire that the magnetic field cuts across, that is, the length of the wire in the motor system's air gap, is represented by l , and RE represents the d.c. resistance of the entire coil. Typically, the coil will be connected to an amplifier which behaves as a voltage source with some small output impedance through a cable which also has some small impedance. For our purposes, the combined influence of these two impedances can be lumped together into an equivalent series resistance, and this is represented by Rg--the generator source resistance. The total d.c. resistance of the system is represented by Rdc and is equal to the sum of RE and Rg. (Note: the voice-coil's impedance also has a complicated inductive-like component associated with it. I have chosen to ignore this in our analysis since the effects of this inductive-like behavior don't manifest themselves at low frequencies.) Viewing the electromagnetic motor this way, we can see that the total force generated by the motor is
where i is the current through the length of wire l. This current will be equal to the voltage sourced to the system divided by the total d.c. resistance, or
Thus,
This isn't terribly important to our task, but it does show the relevance of the often-referred-to "BL product" of a driver. PARAMETER ALTERATION. Having modeled our loudspeaker driver as we have, we now need to figure out what happens to the Fundamental Parameters when we add some mass to the cone or put a resistor in series with the voice coil. I think it's fairly obvious that if we add mass to the cone of our driver, MMD will increase by exactly the amount of the mass that we add. Similarly, if we put a resistor in series with the voice coil, the Rg of the system will increase by an amount equal to the resistance we've added. What is less clear is how the other parameters change, if at all. Let's think about that a bit. Since CMS is a mechanical property of the surround and suspension, neither of our modifications should affect it. Also, since RMS is dominated by the properties of the suspension, it too will remain unaffected. We've done nothing to change SD, which means that MM1 should also stay the same, and since MM1 didn't change, we expect MMS (the sum of MMD and MM1 ) to likewise increase by exactly the amount of added mass. On the electromagnetic side, adding a series resistor will not change the properties of the magnet, so B, the flux density in the gap, stays the same. The added resistor doesn't change the length of the wire in the air gap or the d.c. resistance of the actual voice-coil, so l and RE also stay the same. Since RE stays the same, we expect Rdc to simply increase by the amount of the added resistance. To summarize, when we add an additional mass to the cone of a driver, MMD and MMS increase by the amount of the added mass; when we add a series resistance, Rg and Rdc increase by the amount of the added resistance. All other Fundamental Parameters remain unaffected. This simple result is one reason for performing our analysis based on Fundamental Parameters rather than the more familiar T/S parameters. Rest assured, we'll get around to converting between T/S parameters and Fundamental Parameters soon enough, but first we need to figure out how much mass and/or resistance to add to our driver to get the desired sensitivity using the Fundamental Parameters. BASICALLY SENSITIVE. What we'd like now is an expression for a driver's nominal voltage sensitivity given its Fundamental Parameters. Beranek gives the pressure generated by a loudspeaker diaphragm at low frequencies mounted on an infinite baffle as:
where p is the pressure, Vg is the generator source voltage, r is the distance from the diaphragm to the listening point, f is frequency (in Hz), and RM and XM represent the magnitudes of the real and imaginary parts of the effective load impedance seen in the analogous acoustical circuit from which equation [1] was derived [4]. If we set r to the 1 meter standard and Vg to 2.83 volts RMS (the equivalent of 1 watt into an 8 ohm load), we have a relationship for a loudspeaker's normalized frequency response, S(f):
The parameters RM and XM are cause for some concern since they are rather involved frequency dependent terms that could terminally complicate any additional analysis. Fortunately, if we concern ourselves only with the driver's response above its fundamental resonance, we can employ some more of those acoustician's approximations (the details of which have been excluded for brevity) and use [2] to derive a simple expression for the driver's mid-band voltage sensitivity (referenced to a source voltage of 2.83 volts):
To convert SR to SPL (in decibels), we use:
where pref is the standard reference pressure of 20x10-6 Pa. We can now see from [3] that the system's sensitivity is inversely proportional to both the total d.c. resistance in the system and the total effective moving mass. This may or may not strike you as another surprisingly simple result. We now know, thanks to equations [3] and [4],
how to determine the sensitivity of our driver given its Fundamental
Parameters. Next, we need to know how to calculate the amount of mass
or resistance to add to bring the sensitivity down to the desired level.
Let's call the desired sensitivity (in dB) SPL0'. The amount that the
sensitivity needs to change is
or
Using [3] and letting MMS' and Rdc' represent the total effective mass and the total d.c. resistance of the modified system (i.e., after we've added the mass and/or resistance), we can write:
Substituting the right hand side of [6] into [5b] and rearranging things a bit yields
Similarly, if you let Rdc' = Rdc in [7] (i.e., you don't add any series resistance), you get:
Once you have the modified values for total effective cone mass and d.c. resistance, MMS' and Rdc' respectively, you can compute the actual amount of mass or resistance to add as follows:
where MAKING IT USEFUL. Given a driver of known Fundamental Parameters, we now know how to modify it to produce the desired sensitivity. Unfortunately, most spec sheets and design methods are based on T/S parameters, not the Fundamental Parameters we've been using so far. Our next step, then, is to develop some means of connecting the T/S data speaker builders are accustomed to working with to our Fundamental Parameters. This is turns out to be a lot simpler than it sounds because the T/S parameters are actually based on Fundamental Parameters. I have tabulated a list of equations to use to get from T/S parameters to the Fundamental Parameters in Table 3 and the complementary set of equations to get from Fundamental Parameters back to T/S parameters in Table 4. These equations are simply algebraic manipulations of the relationships published in the standard sources, so I won't belabor you with detailed derivations of each. The equations assume that you know how to determine--or have an accurate spec sheets which specify--the following T/S parameters: VAS, fs (the free air resonance), QMS, QES, and RE (the voice-coil resistance, sometimes called as RVC or something similar). If you are using manufacturer's data in the equation for (B l) in Table 3, you should assume that Rg equals zero unless your data sheet states otherwise. In all cases, use 345 meters/sec. for c, the speed of sound, and 1.18 kg/meter3 for p0 , the mean density of air, unless you have good reason to use other values. It may or may not be interesting to note that the electrical damping and total system damping will change if we add either mass or resistance, that the free-air resonance and mechanical damping will change only when we add mass, and that VAS will not change with either added mass or added series resistance.
Given what we now know, we can define a design process as follows: Take a candidate driver's T/S specifications and convert them to the Fundamental Parameters using the equations in Table 3. Then use equations [3] through [11] above to calculate how much mass and/or series resistance to add to produce the desired sensitivity. Having done that, compute a new set of Fundamental Parameters based on the added mass and resistance, and use the newly computed Fundamental Parameters compute a new set of T/S parameters for the modified driver with the equations in Table 4. Finally, use your favorite cabinet design tools to see what kind of performance you can achieve with the modified driver. Given the sort of "what if" nature inherent in the above process ("What if I add this much mass and this much resistance?") as well as the tedium involved in converting parameters back and forth, you might think that this process would be a good candidate for implementation on a computer spreadsheet. Well, you're right, and you can implement one yourself using the equations presented here. DESIGN EXAMPLE. To show you how to put it all together, I will now perform a design example using a typical catalog driver. Let's say we have a driver that we have determined--either by testing or trusting the manufacturer's data sheet--to have the following T/S specifications: VAS = 30.5 liters, QMS = 1.21, QES = 0.31, QTS = 0.24, fs = 34 Hz, RE = 6.1 ohms, and SD = 130 cm^2. (These are actually the manufacturers' specifications for a commonly available 17cm woofer.) The first step is to convert the T/S data to Fundamental Parameters. Plugging the above T/S parameters into the equations in Table 3 and assuming Rg is zero yields the following Fundamental Parameters for the unmodified driver: CMS = 1.29e-3 m/N, MMS = 17.1e-3 kg, MM1 = 0.84e-3 kg, MMD = 15.4e-3 kg, RMS = 3.01 Ns/m, Rdc = 6.1 ohms, and (Bl) = 8.47 N/A Next, we use equations [3] and [4] to tell us that a driver with the above parameters will have a voltage sensitivity of 88.98 dB--which is the sound pressure level we expect the unmodified driver to produce above cutoff at 1 meter when excited by a 2.83 volt RMS signal while radiating into a hemispherical space. Normally, in a large room and at wavelengths longer than the shortest wavelength of the baffle, a driver effectively radiates into a spherical, rather than a hemispherical, space, and so the actual voltage sensitivity will be one-half (i.e., 6.02 dB lower than) the value calculated with equations [3] and [4]. However, as I mentioned in the introduction to this article, the subwoofer design I had in mind would closely couple the driver to the floor, meaning that the driver would experience boundary doubling, increasing the sensitivity by 6.02 dB over the spherical value. Thus, we expect the sensitivity calculated using equations [3] and [4] to directly predict the unmodified output of our example driver in its actual application. That means for a target sensitivity of 85 dB our example driver's sensitivity must be brought down by 88.98 – 85 = 3.98 dB. WHICH TO ADD? Let us now see what happens when we reduce the sensitivity using series resistance alone. To achieve the 3.98 dB attenuation, equations [8] and [11] tell us that we'll need 3.55 ohms of series resistance. This results in a modified value for Rdc of 6.1 + 3.55 = 9.65 ohms. Plugging this plus the remaining (unchanged) parameters, into the equations in Table 4 yields the following T/S data for the modified driver: VAS = 30.5 liters, QMS = 1.21, QES = 0.49, QTS = 0.35, and fs = 34 Hz. Finally, plugging these values into a low-frequency design program indicates that our modified driver in a ported box of 22 liters tuned to 37 Hz would produce a 3 dB-down point of about 39 Hz. Not bad. Now let's see what happens when we use only added mass to reduce the sensitivity. (In reality this will be difficult to do since the crossover inductors will have a non-negligible resistance associated with them that we should include as an additional series resistance, but the exercise is instructive all the same.) Equations [9] and [10] tell us that 9.9 grams of additional mass will reduce the sensitivity of the driver by the required 3.98 dB. The equations in Table 4 tell us that our new T/S parameters are: VAS = 30.5 liters, QMS = 1.52, QES = 0.39, QTS = 0.31, and fs = 27 Hz. This will let us build a box of 16 liters tuned to 33 Hz for a 3 dB-down point of around 36 Hz. I can live with that. DETAILS, DETAILS. Using a lot of algebra, we can extend the above analysis to eliminate the intermediate conversions to and from Fundamental Parameters and derive a set of equations which directly express the changes in the T/S parameters based on the added mass and resistance. I have chosen not to do so in this article because: (1) The additional work would only marginally extend the utility of what we've just done, and (2) I've probably taxed the patience of even the most dedicated reader already. Still, there are some interesting areas to explore that such an analysis can help with. For example, you might be wondering whether it is generally better to add mass or resistance to lower the sensitivity of a driver. Well, it turns out that from a low-frequency point-of-view it's almost always best to minimize the amount of series resistance you add and to use added mass to achieve the bulk of sensitivity reduction. Such an approach tends to give you the best extension in the smallest cabinet volumes for most typical drivers. Having said that, a word of caution is called for. Adding a blob of mass to a driver's cone will have predictable effects at low frequencies where the cone is moving as a piston. However, at higher frequencies where the cone ceases to behave pistonically, the blob you've added will have completely unpredictable and usually undesirable results. So if you're planning to cross-over the driver above a couple hundred Hertz, use series resistance alone to reduce the sensitivity. The added resistance will itself have some effect on the driver's midrange response as it interacts with the inductive-like component of the voice coil impedance, but the response modifications will tend to be gentle and correctable in the crossover--by adding a Zobel or more complicated network across the voice coil terminals for example. ADDING MASS. Attaching a mass of a few grams to an un-doped paper cone driver should present few difficulties as long as you use high quality adhesives and are careful to not get any of the adhesive on the surround or other moving parts other than the cone. Epoxies in particular seem to be well suited to this task. The mass could come from just about anything--lead shot, plastic beads, even the epoxy itself. On the other hand, getting anything to stick to polypropylene cones is quite another matter. One knowledgeable source has suggested that cyano-acrylates (i.e., "super glues") might work well in this application. Having never tried this, I can make no assurances or additional recommendations. Whatever you end up using, just make sure to include the mass of the adhesive in all your added mass calculations. Clearly, using added mass and resistance techniques can yield systems of significant extension in smallish cabinet volumes if you are designing for a low sensitivity. One often-raised concern regarding deep bass from small enclosures is the non-linear compressibility of air. Colloms indicates that if the compression of the air inside a box exceeds 5% by volume, significant harmonic distortion may result [5]. Let’s see if this will be problem for our 16 liter box using our example driver. The driver has a peak excursion of about 1.0 cm before it bottoms out. The surface area of the cone is 130 cm2, and so the maximum volume displacement is 1.0 * 130 = 130 cm3 or 0.130 liters. This is 0.130/16 * 100% = 0.81% of the total cabinet volume. Clearly, in this case, excursion limitations will have a much, much more pronounced effect on the performance of the system than the non-linearity of air. WHAT ABOUT THE SUBWOOFER? So, how did the subwoofer project fare? I used the spreadsheet mentioned above to investigate many, many drivers in an attempt to find something that looked promising for my subwoofer. Despite the smallish cone area, I eventually settled on the driver used in the design examples above as offering a good compromise between extension and size--especially in view of my space limitations. Unfortunately, after modeling the low frequency impedance of the (modified) driver in an enclosure, it turned out that the cost of equalizing the low frequency impedance peaks--necessary to avoid horrendous crossover mistermination--was irritatingly high. A few second order systems I considered fared little better. In the end, I opted to investigate bandpass loading techniques, and that is the subject of another article. REFERENCES [2] Smith, Brian D., "Adjusting Woofers for High Performance," SB 6/89, pp. 22-24. [3] Beranek, Leo L., Acoustics, 1993 ed., Acoustical Society of America, Woodbury, New York, 1993 [4] Beranek, op. cit. [5] Colloms, Martin, High Performance
Loudspeakers, 1st ed., Wiley, New York, 1978. Small, R. H., "Direct Radiator Loudspeaker Analysis," J. Audio Eng. Soc., June 1972. Small, R.H., "Closed-Box Loudspeaker Systems, Pts I and II," J. Audio Eng. Soc., Dec. 1972 and Jan. 1973. Small, R. H., "Vented-Box Loudspeaker Systems, Pts. I-IV," J. Audio Eng. Soc., June - Oct. 1973. Thiele, A. N., "Loudspeakers in Vented Boxes," J. Audio Eng. Soc., May and June 1971. ACKNOWLEDGMENT * The orignal draft of this article dates back to 1990--long before Biro Technology's birth. Please don't ask why it took seven years to be published.
copyright © 1998 Mithat Konar--all rights reserved |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Site copyright ©2005 Biro Technology–all rights reserved
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
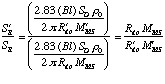 . [6]
. [6]